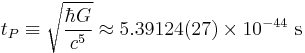Planck time
In physics, the Planck time, (tP), is the unit of time in the system of natural units known as Planck units. It is the time required for light to travel, in a vacuum, a distance of 1 Planck length.[1] The unit is named after Max Planck, who was the first to propose it.
The Planck time is defined as:
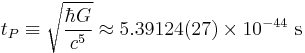 [2]
[2]
where:
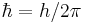 is the reduced Planck constant (sometimes
is the reduced Planck constant (sometimes 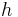 is used instead of
is used instead of  in the definition[1])
in the definition[1])- G = gravitational constant
- c = speed of light in a vacuum
- s is the SI unit of time, the second.
The two digits between parentheses denote the standard error of the estimated value.
Physical significance
The Planck time comes from a field of mathematical physics known as dimensional analysis, which studies units of measurement and physical constants. The Planck time is the unique combination of the gravitational constant G, the relativity constant c, and the quantum constant h, to produce a constant with units of time. For processes that occur in a time t less than one Planck time, the dimensionless quantity 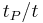 is large. Dimensional analysis suggests that the effects of both quantum mechanics and gravity will be important under these circumstances, requiring a theory of quantum gravity. Unfortunately, all of our scientific experiments and human experience happens over billions of billions of billions of Planck times, which makes it hard to directly probe the events happening at the Planck scale.
is large. Dimensional analysis suggests that the effects of both quantum mechanics and gravity will be important under these circumstances, requiring a theory of quantum gravity. Unfortunately, all of our scientific experiments and human experience happens over billions of billions of billions of Planck times, which makes it hard to directly probe the events happening at the Planck scale.
As of 2010, the smallest unit of time that was directly measured was on the order of 20 attoseconds (10−18 s), or about 3.7 × 1026 Planck times.[3]
Analysis of Hubble Space Telescope Deep Field images in 2003 led to a debate about the physical implications of the Planck time as a physical minimum time interval. According to Lieu and Hillman,[4] speculative theories of quantum gravity "foam" where there are space-time fluctuations on the Planck scale predict that images of extremely distant objects should be blurry. However, blurring was not seen in the Hubble images, which was claimed to be problematic for such theories.[5] Other authors have disputed this, in particular Ng et al.[6], who stated that the blurring effect was overestimated by Lieu and Hillman by factors of between 1015 and 1030, thus the observations are very much less effective in constraining theory: "the cumulative effects of spacetime fluctuations on the phase coherence of light [in certain theories of 'foamy' spacetime] are too small to be observable."
See also
- Orders of magnitude (time)
- Chronon
References
|
Planck's natural units |
|
| Base Planck units |
Planck time · Planck length · Planck volume · Planck mass · Planck charge · Planck temperature |
|
| Derived Planck units |
Planck energy · Planck force · Planck power · Planck density · Planck angular frequency · Planck pressure · Planck current · Planck voltage · Planck impedance · Planck momentum
|
|
|
Time measurement and standards |
|
| Major subjects |
|
|
| International standards |
UTC · UTC offset · UT · DUT1 · IERS · ISO 31-1 · ISO 8601 · TAI · 12-hour clock · 24-hour clock · Barycentric Coordinate Time · Civil time · Daylight saving time · Geocentric Coordinate Time · International Date Line · Leap second · Solar time · Terrestrial Time · Time zone
|
|
| Obsolete standards |
|
|
| Time in physics |
|
|
| Horology |
|
|
| Calendar |
|
|
| Archaeology & geology |
|
|
| Astronomical chronology |
Galactic year · Nuclear time scale · Precession · Sidereal time |
|
| Units of time |
|
|
| Related topics |
|
|
|
Time |
|
| Major concepts |
|

 Time Portal Time Portal |
|
| Measurement and standards |
|
|
| Chronology |
|
|
| Religion and mythology |
|
|
| Philosophy |
A-series and B-series · B-Theory of time · Causality · Endurantism · Eternal return · Eternalism · Event
Perdurantism · Presentism · Temporal finitism · Temporal parts · The Unreality of Time |
|
| Physical sciences |
|
|
| Biology |
|
|
| Psychology |
Mental chronometry · Sense of time · Specious present
|
|
| Sociology and anthropology |
Long Now Foundation · Time discipline · Time use research
|
|
| Economics |
|
|
| Related topics |
Carpe diem · Duration · Hexadecimal time · Metric time · Space · System time · Tempus fugit
Time capsule · Time signature · Time travel
|
|
|
Orders of magnitude (time), by powers of seconds |
|
| Negative powers |
Planck time | <1 attosecond | Attosecond | Femtosecond | Picosecond | Nanosecond | Microsecond | Millisecond
|
|
| Positive powers |
Second | Kilosecond | Megasecond | Gigasecond | Terasecond | Petasecond | Exasecond and longer
|
|
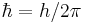 is the reduced Planck constant (sometimes
is the reduced Planck constant (sometimes 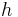 is used instead of
is used instead of  in the definition[1])
in the definition[1])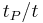 is large. Dimensional analysis suggests that the effects of both quantum mechanics and gravity will be important under these circumstances, requiring a theory of quantum gravity. Unfortunately, all of our scientific experiments and human experience happens over billions of billions of billions of Planck times, which makes it hard to directly probe the events happening at the Planck scale.
is large. Dimensional analysis suggests that the effects of both quantum mechanics and gravity will be important under these circumstances, requiring a theory of quantum gravity. Unfortunately, all of our scientific experiments and human experience happens over billions of billions of billions of Planck times, which makes it hard to directly probe the events happening at the Planck scale.